关于Remeshing的一个简单的定义如下:
- 输入一个3D网格,通过计算得到另一个和输入大致相同且满足一定质量要求网格。
曲面的Remesing目标有以下两点:
- 根据需求减少曲面的复杂度
- 改善曲面的质量(Mesh Quality)
曲面的质量(Mesh Quality) 指的是一些 非拓扑属性(Non-Topological Properties) ,例如采样密度,正则性,大小,方位(Orientation),对齐性(原文为Alignment,不太好翻译),以及曲面网格的形状。
局部结构(Local Structure)
网格的局部结构(Local Structure)说的是网格元素的种类,形状,方位以及分布情况。
元素的种类(Element Type)
最为常用的两个种类是 三角形(Triangle) 和 四边形(Quadrangle) 。
四边形网格可以通过在每一个四边形中插入一条对角线,轻易地转换成三角形网格。
反过来,如果要把三角形网格转换为四边形网格,可以使用重心划分的方法:将三角形的重心和每一条边的中点连接,这样一个三角形就被划分成了3个四边形。另外还有一种方法:将三角形的重心和每一个顶点连接,然后舍弃掉网格上原来所有三角形的边。
元素的形状(Element Shape)
网格的元素可以分为 各向同性(Isotropic) 或者 各向异性(Anisotropic) 两类。
各向同性(Isotropic) 的元素的形状通常在各个方向上一致。理想情况下,当某个三角形(四边形)的元素是或者近似是等边三角形(正方形)时,就说这个元素是各向同性(Isotropic)的。
对于三角形的元素来说,可以通过其外接圆的半径和三边中最短的一条边的比值来度量它具有的各向同性(Isotropic)的强度。

各向同性(Isotropic):右图明显比左图更强
各向异性(Anisotropic) 的元素在网格曲面上各个方向的形状往往都不同,通常这些元素的都朝向(oriented)主曲率的方向。这种元素往往能够更好的表现几何体的结构特征。它的另一个优势在于,相对于 各向同性(Isotropic) ,得到同样质量的网格其使用的元素的个数更少。
元素的密度(Element Density)
在一个平均分布的网格中(Uniform Distribution),网格元素平均的分布在整个模型上。在一个不均匀或者适应性分布的网格中(Nonuniform Adaptive Distribution),每个区域分布的元素的数量都不同,例如比较小的元素通常会较多地处于曲率较高的区域。通过调整,这种不均匀或者适应性分布的网格能够用更少的元素更好地近似出原来的网格。
元素的对齐性和方位(Element Alignment and Orientation)
在Remeshing的过程中,一些尖锐突出的地方(Sharp Features)通常会受到影响产生 走样(Aliasing) ,这些地方的切线是不连续的,为了避免这个情况需要将网格元素与它们(Sharp Features)对齐(Align)。
全局结构(Global Structure)
当三角形网格上非边界上的顶点周围顶点的数量为6或者边界上的顶点周围顶点的数量为4的时候,称这个顶点是 正则(Regular) 的。同理对于四边形网格来说,这两个值对应分别是4和3。
相对于 正则(Regular),其它的顶点则是 非正则(Irregular) 或者 Extraordinary。
网格的全局结构可以根据正则顶点的数目被分为 非正则(Irregular) ,半正则(Semiregular) ,高度正则(Highly Regular) 和 正则(Regular) 四种。
一致性(Correspondences)
所有Remeshing算法,都会在曲面上或者曲面附近计算点的位置。其中大部分算法甚至还会进行额外的迭代来修正顶点的位置以改善网格的质量。所以在Remeshing的过程中一个关键的问题就是要保证计算前后顶点的一致性。
下面有几种解决这个问题的方法:
全局参数化(Global parameterization):将输入的模型整个参数化到一个2维参数域上,然后在这个参数域对采样点的分布和位置进行调整,最后再将其还原到3维空间中。
局部参数化(Local parameterization):算法只保留某个点局部的参数化信息,当采样点变换的时候,再去计算那个点的局部参数化信息。
投影(Projection):将采样点投影到输入模型上对应最近的顶点、边或者三角形上。
全局参数化的计算相对来说比较耗时,同时当模型被切开成一个圆盘(Disk)的时候。
而当采样点离曲面太远的时候,直接进行投影则可能会导致重影现象。通过将对采样点的移动限制在切平面上使得采样点不会原来曲面太远,以解决上述问题。
局部参数化方法相对稳定,并且效果较好,不过需要不断的跟踪记录并重新计算局部的参数化信息。
沃罗诺伊图和德洛内三角剖分(Voronoi Diagrams and Delaunay Triangulations)
沃罗诺伊图(Voronoi Diagrams),简单的说就是基于一组 特定点 将空间分割成不同的区域,而每一个区域都只包含这些点中的一个,并且该区域内的任意点到这个 特定点 的距离 小于 该这个任意点到空间中其它 特定点 的距离。其中这些被分割的区域称作 沃罗诺伊区域(Voronoi Region)。

上面这张图形象的描述了 沃罗诺伊图 的生成过程。
下面我们用数学的形式来表达 沃罗诺伊区域 。给定任意维空间$R_d$上的一个点的集合${\mathbf{p}_1,…,\mathbf{p}_n}$,点$\mathbf{p}_i$的 沃罗诺伊区域 $V (\mathbf{p}_i)$ 是:

沃罗诺伊图 可以看作空间$R_d$上的一个划分,因为该空间上任意一个点必定属于某一个 沃罗诺伊区域 。
与该空间中的任意两个点$\mathbf{p}_i$和$\mathbf{p}_j$等距的点组成的区域被称作 Bisector ,所有的 Bisector 都是该空间上的仿射子空间(Affine Subspace)。例如,在2维空间上Bisector是一条线,3维空间上Bisector是一个面。
从Bisector的定义可以看出,沃罗诺伊区域 也可以被定义为由一些 Bisector 的半空间(Half-Space)相交所围成的闭合区域,因为凸集(Convex Set)相交仍仍然是凸的,所以 沃罗诺伊区域 是一个凸集。不过在靠近整个空间$R_d$边缘的区域,闭合组成 沃罗诺伊区域 的Bisector里就会包含$R_d$的外壳(Hull)部分。
沃罗诺伊图 的对偶结构被称为 德洛内三角剖分(Delaunay Triangulations)。通过连接沃罗诺伊区域内的顶点可以得到其对应的对偶结构,如下图所示:

德洛内三角剖分 的 三角形 $(\mathbf{p}, \mathbf{q}, \mathbf{r})$与 沃罗诺伊区域 $V(\mathbf{p})$,$V(\mathbf{q})$,$V(\mathbf{r})$相交得到的 顶点 对偶。
德洛内三角剖分 的 边 $(\mathbf{p}, \mathbf{q})$与 沃罗诺伊区域 $V(\mathbf{p})$,$V(\mathbf{q})$相交得到的 边 对偶。
德洛内三角剖分 的 顶点 $\mathbf{p}$ 与 沃罗诺伊区域 $V(\mathbf{p})$对偶。
可以发现 德洛内三角剖分 和 沃罗诺伊图 在许多局部和全局的属性上存在对偶关系,如:
对于k维空间上的某个点集$P$上的 德洛内三角剖分 ,其上的任何一个k单纯形(k-simplex:即在$k$维空间上,由$k+1$个点组成的多面体,如2维空间上的三角形,3维空间上的四面等)的外界圆(因为是任意维的情况,所以称作超球面更准确一些)的内部都不包含点集上其它的点。
对于2维空间上的某个点集$P$上的 德洛内三角剖分 ,这种剖分能够最大化所有三角形中最小的角。
另外在进行 德洛内三角剖分 的时候还可以对其加以限制,例如在2维空间上可以用闭合的平面曲线来进行限制,在3维空间上用闭合曲面来进行限制。

蓝色的曲线是作为限制的闭合曲线,红色的直线是与之相交的沃罗诺伊图的边
三角形网格的网格重划分(Triangle-Based Remeshing)
Greedy Remeshing
这个方法的主要思想是对 3维德洛内三角剖分 的 Refining 和提取 Filtering 。
在 Refining 的过程中,输入网格上的点会被选中然后插入到德洛内三角剖分的三角形中。而点的位置则是网格曲面与德洛内三角剖分对应的沃罗诺伊图的边的交点。换句话说沃罗诺伊图的边被用来当作输入网格曲面的“探针(Probe)”。
在 Filtering 的过程中,更新德洛内三角剖分使其被限制在曲面上,即选取德洛内三角剖分的面,与这些面对偶的沃罗诺伊图的边与该曲面相交。
该算法会涉及下面的概念:
Surface Delaunay ball 一个Surface Delaunay ball是一个位于输入网格曲面中心的球,这个球包围了一个德洛内三角剖分中的一个特定的面。一个中心位置为$\mathbf{c}$,半径为$r$,包围了面$f$的Surface Delaunay ball可以记作:

Medial axis 给定n维空间上的一个集合$O$,它的Medial axis $M(O)$是一系列点的集合,以这些点为中心的超球面与集合$O$的边界相切的点的个数至少为$2$。

椭圆区域为O,中间的直线为Medial axis
- Medial ball 中心在Medial axis上的球(ball),其内部被集合$O$包含并且它的包围球面与$O$的边界相交,称这样的球(ball)为Medial ball。

最外侧的实线包含的集合为O,集合内的实线为Medial axis,圆圈所围成的区域为Medial ball
- Reach(Local feature size) 集合$O$内的点$\mathbf{x}$到集合O上的Medial axis的距离称为Reach或者Local feature size。
有了上面的定义就可以准确的描述Refine的过程,即调整带限制的德洛内三角剖分,使得所有的 Surface Delaunay ball 的半径都小于局部的 Reach ,为了保证算法能够正确终止还需要确保 Reach 大于$0$。
算法需要一个点集$P$,$P$的德洛内三角剖分$Del(P)$,带限制条件的德洛内三角剖分$Del_S(P)$,以及$Del_S(P)$中“不好(bad)”的面的列表$L$。
“不好(bad)”的面 的定义为:假定有一个Surface Delaunay ball—— $B_f = B(\mathbf{c}_f,r_f)$,满足$r_f > \Psi(\mathbf{c}_f)$,其中$\Psi$是定义在$S$上的函数,$\Psi$满足下列条件:存在$S$上的一个点$\mathbf{x}$,使得

初始化的时候点集$P$选取$S$中每个联通区域上足够近的三个点,然后执行下面的算法

当$\Psi$满足,其中$\epsilon = 0.2$,$\rho = reach$,上面的算法会在经过有限次的迭代之后终止,并且算法输出的结果——带限制的3维德洛内三角剖分与输入的网格曲面相互同胚。


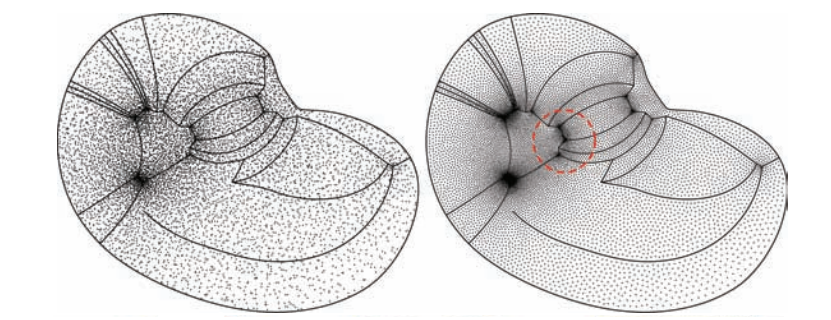
左图为原模型,右图为算法处理后的模型
上述算法由于大量涉及到求直线和三角形面求交的过程,所以可以使用八叉树的数据结构进行加速。
Greedy Remeshing的优点在于其结果保证不会出现自相交,因为三角形网格是取自与三维德洛内三角剖分的。Greedy Remeshing另外一个很好的地方在于他不需要局部或者全局的参数化信息。
那么如果想要使用尽量少的顶点得到质量尽可能高的网格,该怎么做呢?下面的Variational Remeshing方法能够部分解决这个问题。
Variational Remeshing
当我们寻求高质量的网格的时候,就需要对网格进行相应的优化工作。
- 优化的标准是什么? 一些和形状、三角大小等相关的几何量
- 自由度是多少 ?尽可能的少。
Variational Remeshing地主要思想是:将一系列的点尽可能平均地放置到输入地网格之上。
以2D的情况为例,如果要平均地将一系列点放置到一个平面上,其中一个方法就是通过构建一个 Centroidal Voronoi Tessellation(CVT) 来实现。
给定一个边界域$\Omega$,如果存在一个被$\Omega$限制的 沃罗诺伊划分(Voronoi Tessellation) ,其上的任意一个沃罗诺伊区域中的顶点刚好是这个区域的重心,那么称这个这个划分为 Centroidal Voronoi Tessellation(CVT)。
求一个沃罗诺伊区域$V_i$的重心$\mathbf{c}_i$的方法如下:

$\rho(\mathbf{x})$是的密度函数,通常取一个常数(即区域内的质量分布是均匀的)。
Variational Algorithm即变分算法通常需要首先定义一个能量函数,然后通过不断地迭代最小化这个能量函数。
这里我们定义如下地能量函数:

通过观察可以知道,当$\mathbf{p}_i$是对应沃罗诺伊区域$V_i$上的重心的时候,上面的能量函数取最小值。
我们可以使用Lloyd’s Algorithm(也叫Lloyd’s Relaxation Method),通过不断迭代建立一个 CVT 。给定一个密度函数$\rho$和一个点集 $\mathbf{p}_i$,算法由下面三个步骤组成:
- 根据点集$\mathbf{p}_i$建立沃罗诺伊划分(Voronoi Tessellation)
- 计算每一个沃罗诺伊区域的重心$\mathbf{c}_i$,然后将$\mathbf{p}_i$移动到$\mathbf{c}_i$的位置
- 重复执行(1)(2)直到满足收敛条件

从左到右:原始的沃罗诺伊划分;经过一次迭代后的划分;经过三次迭代的划分;Centroidal Voronoi Tessellation(CVT)
为了能够在3D网格上应用同样的算法,我们先将网格进行保角参数化,然后在参数空间上应用Lloyd’s Algorithm。参数化的过程中会导致三角形变形,密度函数 ρ 在这里就被用来抵消这种变形,通过在多个带边界限制的沃罗诺伊图上分别应用Lloyd’s Algorithm,网格上一些诸如褶皱、夹角的特征能够得到保留。
Incremental Remeshing
Incremental Remeshing相较于之前的Variational Remeshing来说实现起来更加简单——它不需要进行参数化并且不需要进行划分(Tessellation)。
算法首先输入一个目标边长(Target Edge Length),然后根据这个输入对网格中较长的边进行Split操作,对较短的边进行Collapse操作,并且会移动顶点的位置,直到所有边的长度和输入的目标边长(Target Edge Length)大致相当。算法的伪代码如下:

注意到我们通过输入的长度得到一个区间$[low, high]$,如果边长在区间左侧则认为这条边太短需要进行Collapse操作;如果边长在区间的右侧则认为这条边太长,需要进行Split操作。

网格的基本操作
split_long_edges(high) 函数会遍历当前网格中所有的边,如果其长度大于high,那么我们就从这条边的中点对其进行Split操作。操作之后,和这条边相邻的两个三角形都会被一分为二。

collapse_short_edges(low, high) 函数同样对当前网格的所有边进行遍历,对长度小于low的边进行Collapse操作。不过需要注意的一点是,在进行Collapse操作的时候需要检查经过该操作是否会产生长度大于high的边,如果不产生,那么我们进行此次的Collapse操作,否则不进行。

equalize_valences() 函数对边进行Flip操作来调整各个顶点的Valence(于该顶点相邻的顶点的个数),使其尽量地接近目标Valence。函数会遍历当前网格的所有边,并尝试对其进行Flip操作,然后比较Flip操作前后和这条边相邻的两个三角形上的四个顶点其Valence和目标值的偏差,如果偏差没有变小那么撤销之前的Flip操作(对这条边再进行一次Flip操作)。
target_val(v) 函数接受一个顶点做为输入,如果该顶点是边界上的点那么函数返回4,如果是内部的点则返回6。

tangential_relaxation() 函数对当前的网格进行反复的平滑过滤。假定$\mathbf{p}$是网格上的某一个点,$\mathbf{n}$是该点的法线量,然后使用下面的方法计算出点$\mathbf{q}$ :

然后我们将$\mathbf{q}$向$\mathbf{p}$点的方向投影,得到$\mathbf{p}$的新位置:


project_to_surface() 函数将顶点投影到原曲面上。
为了保证输入模型的特征,在进行上面的算法的时候需要加入一些限制:
角上的顶点(Corner Vertices)对应的一个或两个特征边(Feature Edge)必需被保留,并且不对其进行任何可以改变其几何或者拓扑结构的操作。
对一个特征边(Feature Edge)进行Split操作将得到两个特征边(Feature Edge)和一个特征点(Feature Vertex)。
对特征边(Feature Edge)进行 tangential_relaxation() 函数的时候,只能在这条边的方向上进行。
对处于特征边(Feature Edge)的点进行Collapse操作的时候只能在沿着这条边的方向上进行该操作。
不能对特征边(Feature Edge)进行Flip操作
四边形网格的网格重划分(Quad-dominant Remeshing)
生成四边形网格的思路主要有下面几种:
四边形化(Quadrangulation):通过放置一些列的点,然后将其四边形化(通过添加Steiner Point或者使用Circle Packing法)。不过缺点在于缺乏对边朝向性(orientation)和对齐性(alignment)的控制。
转化(Conversion):首先生成三角形网格或者多边形网格,然后将其转换维四边形网格。转换的具体方法有:合并与一条边相邻的两个三角形 ,切分多边形网格等。这种方法能够简单地控制边的朝向性和对齐性。
基于曲线的采样(Curve-based Sampling):通过放置一系列与方向场相切的曲线来生成一个曲线网络,这样网络上的每一个交点正好是生成的顶点。此方法能够很好的控制边的朝向性和对齐性,不过生成的四边形网格上可能会有T-Junction,所以并不完全是一个四边形网格。

T-Junction
- 等值线法(Contouring):一个能得到纯四边形网格(Pure Quadrangle Mesh)的方法包含有如下:计算两个标量函数、将经过选取的一系列等值带入这两个函数中从而得到四边形网格的一些列小四边形。
这里我们将讨论的方法基于后两点,该方法包含三个主要步骤:
- 首先计算每个顶点的曲率张量(Curvature Tensor)来还原出一个连续(continuous)的模型。计算完张量之后,丢弃掉其中法向量的分量。然后通过计算离散保角参数化(Discrete Conformal Parameterization)得到了一个2维分段张量场,然后对其使用高斯核函数做卷积运算,得到一个平滑的曲率方向场,并且提取出张量场中的脐点(Umbilics)。

曲率张量

左图:初始主方向场;右图:平滑后的主方向场;图中彩色的点为脐点
- 第二步是在参数空间上上进行重新采样。对于各向异性的区域(Anisotropic Area),建立由一些列曲率线(沿着主曲率的方法)组成的网格;而对于各向同性的区域(Isotropic Area)则使用普通的顶点采样的方法

- 最后一步通过第二部采样出来的点获得边,在各向异性的区域我们将曲率线拉直以得到边,在各向同性的区域我们通过德洛内三角剖分来获得边。最终得到的多边形网格中既包含三角形也包含了四边形。
不过对于平坦的区域,由于曲率线之间的距离很大,可能最后不会产生任何的多边形。因此当曲率线进入一个较为平坦的区域的时候,算法使从其上一个采样点开始沿着测地线(Geodesic Curve)的方向延长,直到其进入较为弯曲的区域。